President's Message - September 2008

Teaching and Learning Mathematics - Teachers and Students Making Connections

In the summer of 1960, 26-year-old Jane Goodall did the unthinkable - she arrived on the shore of Lake Tanganyika in East Africa to study the area's chimpanzee population. A courageous and dangerous venture, Jane was determined to fulfill her childhood dream.

Initially, the wild animals fled from the young researcher out of fear for the human invader. It would take Jane months to get close to the chimpanzees, forcing her to observe the animals at a distance through binoculars from a peak overlooking the forest. Gradually, Jane was able to find a way to connect with the chimpanzees, forming a bond that would allow her to make some of the most important discoveries of chimpanzee behaviour by a field researcher to date.

This type of connection, critical to Jane's work is also critical to us as teachers as we strive to connect students to the realm of mathematics. As we embark on a new school year and begin the planning and preparation required, we need to reflect on how we can make these connections meaningful and relevant.

As Arthur Hyde noted, "Making connections is at the heart of doing mathematics." But the question remains how do we help students connect to the mathematics they are learning at school? As a starting point we can turn to Comprehension Connections - Bridges to Strategic Reading by Tanny McGregor 2007, which describes a way of organizing the different connections students can make with the text they are considering.

The Concentric Circles of Connection

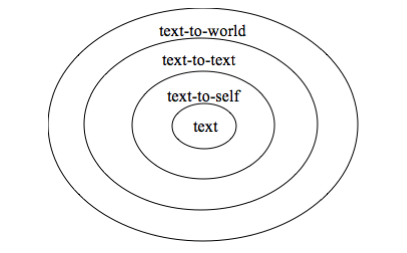
When students make text-to-world connections they think of the big ideas, themes and/or the world around them. As they make text-to-text connections, students relate to texts or media and then ultimately their own lives during text-to-self connections.

What do these connections look like when it comes to mathematics? Can students make connections to make mathematics come alive in a way that is relevant to them? For this to happen, we need to find ways of connecting math to the real world, to what they already know and to their personal experiences.

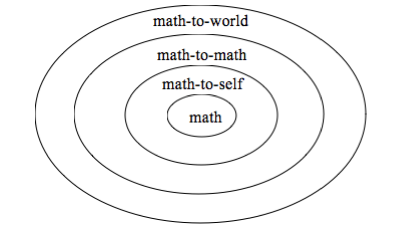
Math-to-world connections help students identify real world applications of the math they are studying in the classroom. Students would consider the big ideas in the mathematics and see how math relates to other subject areas such as the sciences, and media literacy. Math-to-math connections have students think about how the strands/courses are related, how problems or situations are similar and how connections can also help them understand how concepts and procedures are related. Math-to-self connections give students the opportunity to make personal connections, apply prior knowledge and experience to new problems or situations.

As teachers, our role is to help establish these connections in a way that makes sense to the diverse student population we serve.

Consider Jane Goodall's theory of making connections:

Do you have a dog? Suppose he wants to go outside. How does he ask? Does he bark or whine at the door while looking at you? That's easy to understand. But dogs can ask in other ways. Perhaps he or she comes up to you (or another member of your family) and lays his head on your knee. Or he looks at you, gives a tiny whine, and wags his tail. Or he starts to pant, getting louder and louder. Or he becomes restless and walks about a lot. . . Dr. Doolittle's parrot, Polynesia, tells us that in order to learn animal language we must have "powers of observation." We must be able to notice "small things about birds and animals - the way they walk and move their heads and flip their wings, the way they sniff the air and twitch their whiskers and wiggle their tails.

Similarly, as teachers of mathematics we must carefully observe and question our students and use this connection to make instructional decisions.

• Using developmentally appropriate, conceptually rich problems that are focused around the big ideas in mathematics will provide students opportunities to use their prior knowledge and apply concepts and skills across strands or units of study.
• Using contexts that are relevant to the different ages and stages of development will allow students to make math-to-world and math-to-self connections.
• Using different forms of technology including, computers, calculators, interactive white boards and others will not only provide for differentiated instruction, but will also connect students and the mathematics at school with our technological society.

An elementary teacher's recent reflections express the student benefits of making connections:

Making math meaningful, helping students make connections can make a significant impact in their ability to apply knowledge in a multitude of ways. The excitement and curiosity from meaningful mathematics can fuel the mind of a student beyond anything they thought possible. - Andrew Schmitt

For Jane Goodall, her drive and determination to make that connection fuelled her findings and set her along a path of unparalleled discoveries. As teachers if we can make meaningful connections like this with our students and aim to help them connect with the mathematics they are learning they are bound to reap the benefits well into the in the future.

Previous Message:
Connecting the dots. Who would have thought that it was so important?

Next Message:
Change in Mathematics Instruction and Student Success: A look at both sides of the equation

Index of Messages