President's Message - March 2005

Imaging

GORDON COOKE

gordonbcooke@gmail.com

I found the following at www.ldonline.com in an article by Nanci Bell
"Why can't everyone think with numbers? Why do some children learn math readily, handle money and time concepts with ease, retain information from year to year, and think with numbers effortlessly? What cognitive processes do some have that others do not?

Mathematics is cognitive process-thinking-that requires the dual coding of imagery and language. Imagery is fundamental to the process of thinking with numbers. Albert Einstein, whose theories of relativity helped explain our universe, used imagery as the base for his mental processing and problem solving. Perhaps he summarized the importance of imagery best when he said, "If I can't picture it, I can't understand it." For the people who "get" math, the language of numbers turns into imagery. They use internal language and imagery that lets them calculate and verify mathematics; they "see" its logic.

Imaging is the basis for thinking with numbers and conceptualizing their functions and their logic. The Greek philosopher Plato said, "And do you not know also that although they [mathematicians] make use of the visible forms and reason about them, they are thinking not of these, but of the ideals which they resemble…they are really seeking to behold the things themselves, which can be seen only with the eye of the mind?"

This certainly describes some of the efforts of a group of Ontario teachers who came together in another of Tom Steinke's summits. This time we were working on authoring GSP sketches which could be used to help remediation efforts in areas other than Geometry. Led by Nick Jackiw and Nathalie Sinclair the group was taken along a learning journey that included technical aspects of sketches and pedagogical considerations on how to use the sketches in a remedial setting.

One of my favourites was a simple activity called Jump Along. Students set two parameters: n jumps of size m. Animation produces n semicircular jumps on a number line. Here is an investigation into the ways to get to 12.

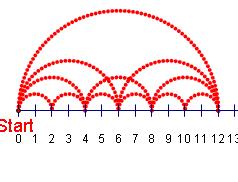
Questions like, What do prime numbers "look like"? and What kind of numbers have jump paths that don't cross each other? help students make the kind of image/language connections referred to in the Bell article.

To see the results of the summit, go to www.vlearning.ca and follow the links to the PRISM sketches. Happy imagining.

Previous Message:
Remediation

Next Message:
Greetings! And A Special Welcome To New OAME Members!

Index of Messages